境界線は垂直な線か水平な線か４５度の線の折れ線になります。面白いですね。
●特徴的な配置の場合の図
母点が正方形を形成するように配置されている場合のボロノイ図
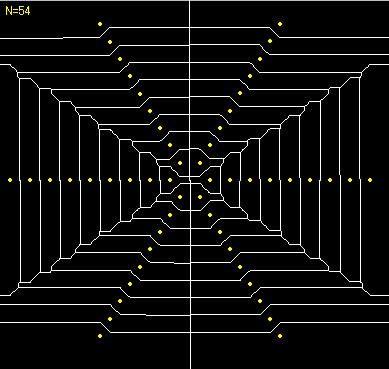母点が放射状に配置されている場合のボロノイ図1
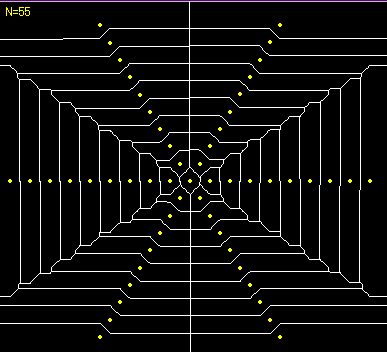母点が放射状に配置されている場合のボロノイ図2
母点が正三角形を形成するようにに配置されている場合のボロノイ図2
母点が正六角形を形成するようにに配置されている場合のボロノイ図2●応用
碁盤の目のような道路のネットワークがある地域で施設の圏域を知りたい時に使えます。
アルゴリズムの概要
こちらのボロノイ図のページで紹介している描き方を流用してマンハッタンボロノイ図を描くことができます。
以下は普通のボロノイ図の描き方の概要です。
i=1,...,N-1
j=i+1,...,N
p(i)とp(j)の境界線（普通のボロノイ図では垂直二等分線）を考えます。
k=1,...,N ただし i,j以外
p(i)とp(k)の境界線を考えます。
(i,j)の境界線と(i,k)の境界線の交点を計算します。
next k
交点の配列にi,jの境界線のx=0とx=(画面の幅)の点を追加します
ｘ座標の小さい順に交点を並び替えます。
k=1,...,交点の数
cを交点と次の交点の中点とします
dをd(c,p(i))とします。（普通のボロノイ図ではdはユークリッド距離。マンハッタンボロノイ図ではマンハッタン距離）
h=1,...,N ただし i,j以外
d'をd(c,p(h))とします
If d'<d then アウトです
next h
If アウトでなければ, then 交点と次の交点を結びます。
next k
next j
next i
これを流用するのですが、ポイントはマンハッタンボロノイ図の境界は直線ではないということです。
すなわち、水平な半直線、斜め４５度の線分、水平な半直線(これをタイプ１とします) or
垂直な半直線、斜め４５度の線分、垂直な半直線(タイプ２とします)
(See Okabe et al. Soatial tessellations 2nd ed. Fig. 3.7.2)
この組み合わせのタイプは点iと点jのｘ座標の差とｙ座標の差の大小関係により決まります。
すなわち、ｘ座標の差がｙ座標の差よりも大きければタイプ２で
ｙ座標の差がｘ座標の差より大きければタイプ１です。
(なお、差が等しい場合は考慮しておりません。乱数を使って母点を作成しているので、厳密に等しくなることはないので・・・)
それから、ここでは裏技として、タイプ２で登場する垂直な半直線（ｘ＝？という直線）をｙ＝400ｘ＋？としています。
ちょっと反則だとは思いますが、見た目的にOKなのでお許しください。
以上が概略になります。
●プログラムのダウンロード(man.java 70KB)ご意見、ご感想、お問い合わせ、お願い等がございましたら、お気軽に、
メール送信フォームからメールを送るか、●掲示板に書き込むか、
どちらかお好きな方法で、ご連絡お願いいたします。
●大山崇のホームページの利用について
●大山崇のホームページ