ボロノイ図(Voronoi diagram)は、平面上にいくつか点が与えられた時、各点に領域を割り当てるための図です。
点sと点tの距離をd(s,t)とします。
今、N個の点p(1),p(2),...p(N)があるとき、p(i)のp(j)に対する優位領域Dom(p(i),p(j))を、d(x,p(i))の方がd(x,p(j))より小さいxの集合とします。そして、iでないj全てでDom(p(i),p(j))を作り、その積集合をとったものをp(i)のボロノイ領域と呼ぶことにします。この時、p(1),...p(N)のボロノイ領域を表したのがボロノイ図です。
ここで、dの決め方によって、さまざまなボロノイ図ができます。上で示している普通のボロノイ図は距離d(x,p(i))を、
d(x,p(i))=普通の距離(定規ではかる距離)
と定義します。この場合、境界線は二つの点の垂直二等分線の一部になります。また、多角形の頂点は３つの線分の交点になります。
ちなみに各点の圏域の面積はボロノイ領域の面積となります。
さらにちなみに、母点が正方形を形成するように並んでいる場合、下図のようになります。
さらにちなみに、点の配置をもっと特別にすると、次のようにもなります。
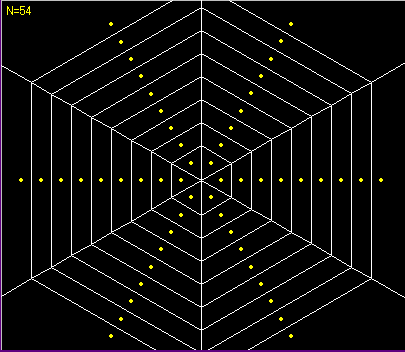蜘蛛の巣を連想させるボロノイ図1
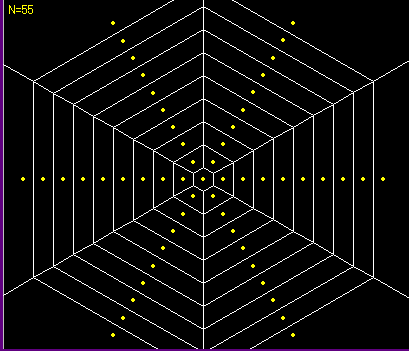蜘蛛の巣を連想させるボロノイ図2
ハチの巣を連想させるボロノイ図
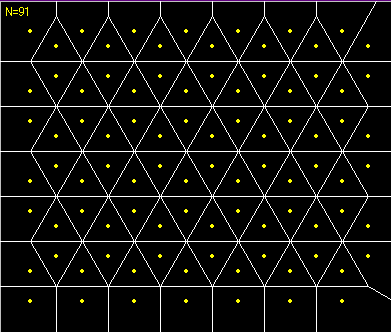正六角形を形成する母点によるボロノイ図●応用
・各点を学校と見なして、学区を決めることができます。
・各点を消防署や警察署と見なして、その管轄を決めることができます。
・空円・最大空円問題
●上の説明はわかりにくいので、参考書の紹介。
A.Okabe、B.Boots、K.Sugihara著、WILEY社、SPATIAL TESSELLATIONS
岡部篤行、鈴木敦夫著、朝倉書店、最適配置の数理
伊理正夫監修、腰塚武志編集、共立出版、計算幾何学と地理情報処理
また、ボロノイ図のページとして、次をお勧めします。是非、アクセスしてみてください。
●もりごんの足跡
・もりごんのボロノイ図のJAVA実験へのショートカット
・もりごんのかち割りダイヤモンドへのショートカット
●プログラムのダウンロード
○Java(voro.java 6KB)
○MS Visual Basic(vbvoro.lzh)
●プログラムの説明
プログラムの簡単な流れは、
１、あらゆる２点の垂直二等分線をひいてください。（本当にはひかず、薄く）
２、１本の垂直二等分線に着目します。
その垂直二等分線は、いくつかの別の垂直二等分線とまじわっています。その交点をやはり、ソートしてください。そうすると、垂直二等分線が、いくつかの線分になります。(右端、左端も９９９９等と適当に与えてください。)
３、そのすべての線分について、線分内の点(ex, 中点)とすべての生成点との距離をはかり、垂直二等分線を作った点が１，２番目(厳密にはどちらも１番目)に近ければ、その線分を引きます。
４、これをすべての垂直二等分線について行います。
次にVisual Basicのvoro1.frmのプログラムで説明します。
３１ー３３行はユークリッド距離を与える関数です。
３５ー９１はヒープソートという、小さい順に並べ替える関数です。ここでは、ｓ１の小さい順に並べ替えます。
１２７のＮＮＮが生成点の数です。
１３１ー１３６で座標を乱数で与えています。
１３７では原点からの距離が近い順に並べ替えていますが、見た目をきれいいにするだけで、必要はありません。
１３８ー２４１が作図の本体です。
i=1,...,N-1
j=i+1,...,N
i,jで垂直二等分線を考えます。
k=1,...,Nただしi,j以外
i,kの垂直二等分線を考えます。
i,jとi,kの線の交点を求めておきます。
next k
i,jの垂直二等分線のx=0の点とx=(画面の幅)の点を交点の配列に追加します。
交点をx座標の小さい順に並べ替えます。
k=1,...,交点の区間数
区間の中点をcとしますが、
cとiの距離をdとします。
h=1,...,Nただしi,j以外
hとcの距離d'とします。
d'<dなら、”駄目”というラベルを与えます。
next h
駄目でなければ、区間の線分をひきます。
next k
next j
next i
が大体の流れです。本プログラムでは若干の高速化も行っていますが、ここでは説明を省略させていただきます。
ご意見、ご感想、お問い合わせ、お願い等がございましたら、お気軽に、
メール送信フォームからメールを送るか、●掲示板に書き込むか、
どちらかお好きな方法で、ご連絡お願いいたします。
●大山崇のホームページの利用について
●大山崇のホームページ